Cum sa nu scriem solutiile problemelor

Rezolvarea unei probleme de fizica nu inseamna utilizarea la nimereala a unor formule invatate pe dinafara. Din pacate, aceasta perceptie este creata si sustinuta prin modul in care unii profesori redacteaza solutiile problemelor. Ecuatiile sunt trintite pe pagina fara nici un fel de justificare, figurile explicative lipsesc sau sunt primitiv executate, semnificatia unor variabile nu este precizata sau este gresit alocata. Stilul acesta este vizibil, prin excelenta, in solutiile si "baremele" de la bacalaureat si diverse concursuri. Mai mult, in unele cazuri, ca formulele sunt aruncate de autor fara sa stie de ce se pot aplica in situatia data este nu doar o impresie, ci este trista realitate. Exemplificam, in continuare, cu o problema data la Olimpiada Nationala de Fizica, Satu Mare, 2013, propusa de Liviu Arici, profesor la Colegiul National "N. Balcescu" din Braila. Vom discuta solutiile propuse de autor la citeva dintre punctele problemei.

Fie o coarda elastica orizontala, intinsa, la capatul careia se produce o mica perturbatie brusca pe directia transversala pe coarda.
1.a. Sa se demonstreze ca viteza de propagare a acestei perturbatii prin coarda este c=η √(F/μ), unde F este tensiunea mecanica din coarda, iar μ – densitatea liniara de masa.
1.b. Ce expresie are constanta η din formula de mai sus?

Iata solutia propusa de autorul problemei:


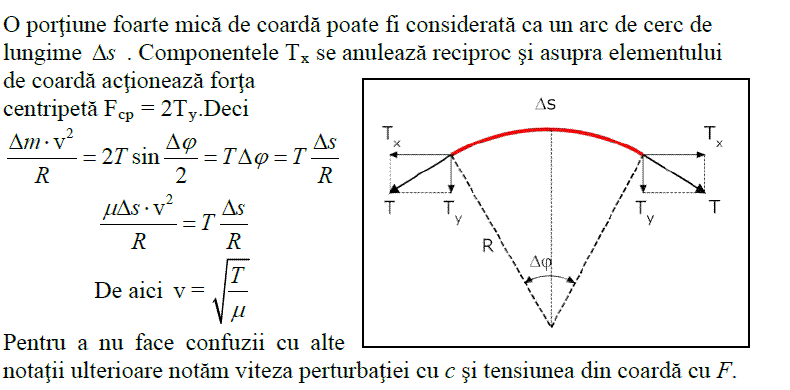
Utilizarea formulei accelaratiei centripete a unui punct material care se misca cu viteza v   pe o traiectorie circulara de raza R apare aici, fara nici un fel de justificare.

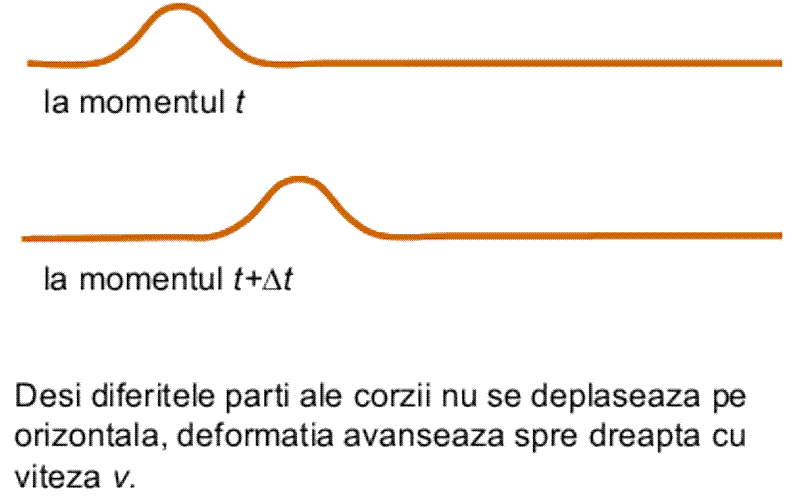
Prezentam, in continuare, rezolvarea problemei, argumentind detaliat fiecare pas. Stim, de la studiul undelor, ca perturbatia produsa se va deplasa, pastrindu-si forma, fara ca portiunile corzii sa se deplaseze pe orizontala, ca in figura urmatoare.

In situatia din figura, deformarea se deplaseaza spre dreapta cu viteza v. Evident, toate afirmatiile de pina acum sunt valabile intr-un sistem de referinta legat de Pamint, sistem in care dispozitivul ce sustine coarda este in repaus. Sa analizam cum se vad lucrurile intr-un sistem de referinta care se misca spre dreapta cu o viteza constanta, egala exact cu viteza v. In acest sistem, deformatia apare ca fiind in repaus. Pe de alta parte, coarda "curge" de-a lungul formei sale, spre stinga, cu viteza v.


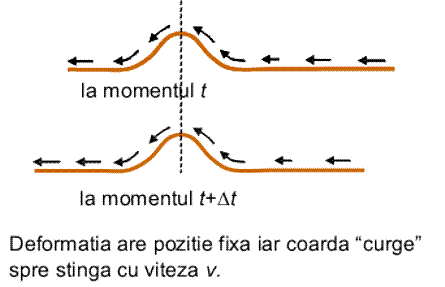
Noul sistem de referinta este si el unul inertial, legile mecanicii putind fi aplicate. Vom analiza miscarea unei portiuni mici de coarda care a ajuns in "virful" deformarii (figura de mai jos, stinga).


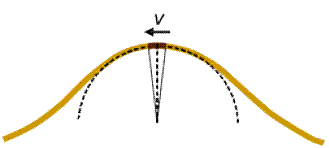
Aceasta are viteza v orizontala, orientata spre stinga dar traiectoria este curbata datorita unei acceleratii centripete. Miscarea poate fi considerata, in acel moment, ca una circulara, fara acceleratie tangentiala, pe un cerc tangent la forma coardei. Asupra acestei portiuni de coarda, de masa Δm si lungime Δs actioneaza restul corzii cu forte de tensiune, egale in modul cu T.


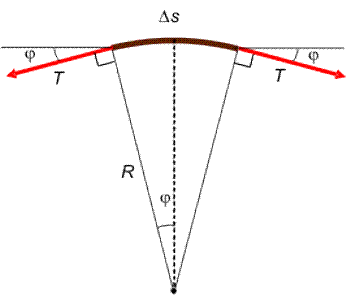
Rezultanta lor este pe directie verticala si, pentru ca unghiul subintins de Δs este foarte mic, marimea acestei rezultante, 2T sin(φ), se obtine ca TΔs/R, R fiind raza cercului care aproximeaza traiectoria. Pe de alta parte, acceleratia centripeta este v²/R iar Δm =μΔs. In final, scriind legea fundamentala a dinamicii, rezulta expresia vitezei v ca fiind radical din T/μ. Dar aceasta este chiar viteza de deplasare a perturbatiei produse pe coarda.

Intelegem ca spatiul redus pe care l-a avut la dispozitie autorul problemei pentru scrierea solutiei nu i-a permis explicatii detaliate, ca cele de mai sus, dar specificarea sistemului de referinta in care sunt valabile ecuatiile pe care le scrie era obligatorie, pentru ca acel sistem de referinta nu este cel obisnuit (Pamintul) ci unul special, ales in asa fel ca perturbatia sa apara ca fiind in repaus.

Sa discutam, acum, alte doua puncte ale problemei propuse la Olimpiada mai sus mentionata.

Dupa autor, rezolvarea ar fi:

Identitatea trigonometrica invocata e valabila oricind si nu are legatura cu conditiile de la capetele coardei. Ea spune doar ca din suprapunerea a doua unde avind amplitudini egale si frecvente egale, una progresiva si una regresiva, rezulta o unda stationara. Ecuatia data este valabila pentru cazul in care capatul din stinga este liber, deoarece acolo factorul cu dependenta spatiala este 1 si avem un ventru (daca, evident, originea axei a fost luata la capatul coardei). Pentru ca si oscilatia data sa fie valabila si in conditiile in care celalalt capat este liber, trebuie ca si acolo sa existe un ventru, adica vectorul de unda k sa fie un numar intreg de π/L  unde L  este lungimea pe care o are coarda. Ceea ce autorul considera a fi o rezolvare nu este decit o formula matematica utila, care putea fi data, la urma urmei, chiar in textul problemei.

La punctul 2.d al problemei se cere calcularea densitatilor liniare ale energiei cinetice si energiei potentiale, in conditiile in care ecuatia de miscare este cea data la punctul 2 a. Determinarea energiei cinetice a unei mici portiuni de coarda nu prezinta dificultati conceptuale. Este necesara cunoasterea vitezei (orientata pe axa y) la pozitia x fixata. Daca derivam pe y in raport cu timpul, obtinem usor expresia densitatii de energie cinetica

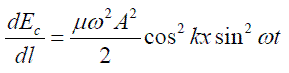
Calcularea energiei potentiale datorata deformarii produse de oscilatie este, insa, mult mai delicata. Deoarece miscarea se face numai pe verticala, portiunea cu lungimea Δx  a corzii initial orizontale ajunge, la un moment de timp sa fie inclinata cu unghiul α si sa aiba lungimea Δl , ca in figura de mai jos.


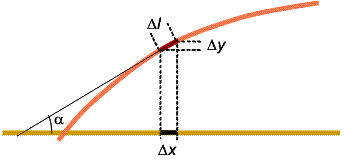
Alungirea suplimentara a acestei portiuni este, deci, δ=Δl -Δx  (sa nu uitam ca exista deja o alungire initiala a acestei portiuni, mult mai mare, produsa de tensiunea T in pozitia orizontala). Aceasta crestere mica a alungirii nu modifica semnificativ tensiunea, astfel incit energia potentiala suplimentara primita de aceasta portiune se poate scrie simplu ca produsul dintre tensiune (aproximativ constanta) si alungirea suplimentara ΔE_P =T ^.δ.
Deoarece unghiul α este foarte mic si 1-cos(α)=2sin²(α/2), obtinem energia potentiala a portiunii considerate, datorata deformarii produsa de oscilatie, ca TΔx ^.α²/2. Mai ramine sa calculam unghiul α pentru o pozitie x oarecare. Acesta este aproximativ egal cu tangenta sa, adica cu panta graficului y(x), egala cu derivata lui y in raport cu x. Rezulta in final ca densitatea liniara de energie cinetica are expresia


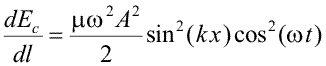
Si acum, daca am inteles ce si cum calculam, sa privim rezolvarea propusa de autorul problemei:


Expresia deformatiei relative este trintita fara nici o justificare. De fapt, ceea ce numeste autorul "deformatie relativa" este panta graficului y(x) (inclinarea portiunii de coarda), notata de noi cu α. Alungirea relativa a portiunii considerate (alungirea raportata la lungimea initiala) este jumatate din patratul pantei. Si este alungirea suplimentara, provocata de deformarea data de y(x). Ca sa-i iasa rezultatul dorit, autorul mai face o sarlatanie: scrie legea alungirii elastice cu dl si energia potentiala cu dy, cu aceeasi constanta elastica. Oricare ar fi semnificatiile pentru dl si dy (in lipsa unui desen plutim in necunoscut), aceste doua expresii nu pot fi valabile simultan. In concluzie, rezolvarea propusa de domnul profesor este bazata pe amestecul la intimplare a unor formule, unele dintre ele fiind contradictorii, si pe confuzia dintre tangenta unui unghi si alungirea relativa a portiunii de coarda care este considerata in calcul.